Mit Mathematischer Optimierung die richtigen Entscheidungen treffen

Entscheidungsunterstützung entlang der Supply Chain

Das Besondere am ADA Lovelace Center ist die Verknüpfung von Kompetenzen der KI-Forschung mit praxisnahen Applikation. So forschen die Wissenschaftler nicht nur in einer Kompetenzsäule wie »Sequenzbasiertes Lernen«, »Data-centric AI« oder »Vertrauenswürdige KI«, sondern nutzen die Methoden in verschiedenen praxisnahen Fragestellungen und entwickeln sie anhand derer weiter.
Ich freue mich, Ihnen heute wieder einen Beitrag eines Experten des ADA Lovelace Center rund um seinen Forschungsschwerpunkt präsentieren zu dürfen. Julius Mehringer leitet die Applikation »Adaptive Selbstoptimierende logistische Netzwerke« und entwickelt geeignete mathematische Optimierungsmodelle, um Entscheidungen bezogen auf ein komplexes Gesamtsystems zu ermöglichen.

Tauchen Sie ein in die Welt der »Mathematischen Optimierung« und wie sie hilft innerhalb komplexer Geschäftsprozesse optimale Entscheidungen zu treffen!

Prognose und mathematische Optimierung in praktischer Anwendung

Entlang der Supply Chain sind ständig unternehmerische Entscheidungen zu treffen, um definierte Geschäftsziele zu erreichen. In vielen Fällen müssen dabei Entwicklungen der Zukunft abgeschätzt werden, um darauf basierend gute Planungsentscheidungen treffen zu können. Fragen wie »Wie wird die zukünftige Nachfrage sein?« oder »Um diese wahrscheinliche Nachfrage zu decken, wie müssen wir unsere Produktion planen?« lassen sich im Forschungsfeld Prescriptive Analytics zusammenfassen – der kombinierte Einsatz von Prognose und Optimierung zur Entscheidungsfindung.

Optimale Produktionsplanung bei Mischprodukten

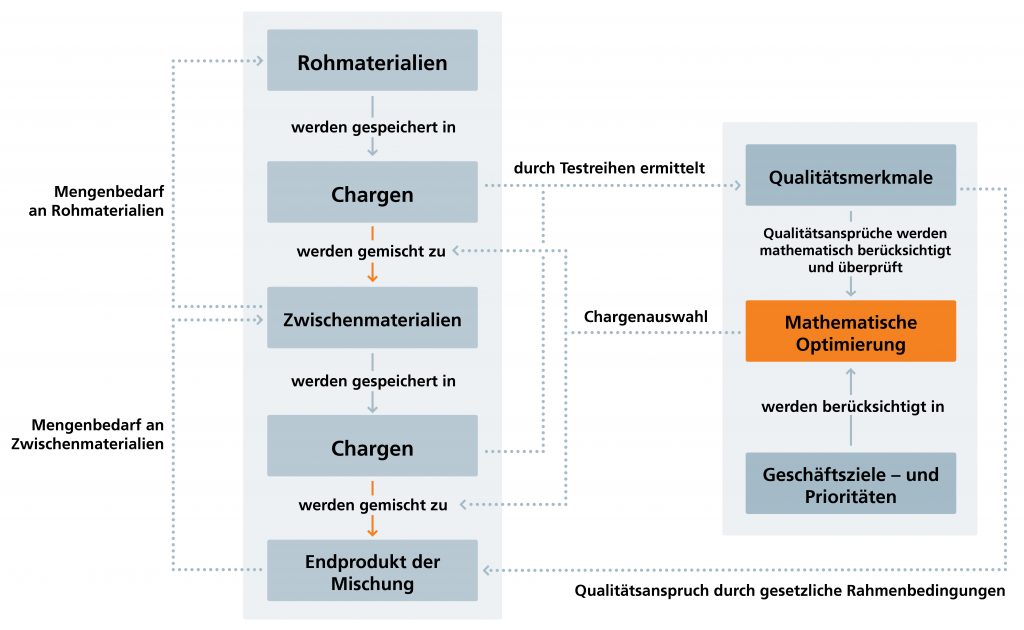
Lassen Sie uns im Folgenden eine modellhafte Supply Chain innerhalb eines produzierenden Unternehmens in der verarbeitenden Industrie betrachten. In diesem Modellunternehmen wird durch das Mischen von Rohmaterialien ein Produkt erzeugt, welches eine gleichbleibende Güte aufweisen soll. Im ersten Schritt gilt es, das Mischproblem so zu lösen, dass das Ergebnis in akzeptabler Schnelligkeit zur Verfügung steht. Dazu wurde die mathematische Struktur des Problems untersucht und identifiziert, wie die Lösung beschleunigt werden kann.

Produktionsbereichsabhängige Rahmenbedingungen und kundenspezifische Prioritäten und Ziele verleihen dabei dem mathematischen Modell individuellen Charakter. Unterschiedliche Geschäftsziele, wie beispielsweise maximierte Auftragsabdeckung, baldige Verwendung von Roh- bzw. Zwischenmaterialchargen, deren Qualität bei weiterer Lagerung potenziell abnehmen könnte, können in einer Kette von aufeinander aufbauenden Modellen priorisiert berücksichtigt werden.

Die Ergebnisse der mathematischen Optimierung bieten dem Produktionsplanenden eine wertvolle Entscheidungsunterstützung und erwirtschaften folglich eine Zeit- und Kostenersparnis für das Unternehmen. Darüber hinaus ermöglicht die vorausschauende Planung eine nachhaltigere Lagerführung.

Prognose der Produktnachfrage

Desweiteren soll auch die Nachfrage der Produkte prognostiziert werden, da bisher der Planungsprozess basierend auf Heuristiken erstellt wird. Je nach Charakteristik der Nachfragemuster kommen hier unterschiedliche Methoden in Frage, die mittels statistischer Verfahren oder maschinellem Lernen erlernt werden können (bspw. Exponential Smoothing (ETS) oder tiefe autoregressive Modelle (DeepAR)). Ein besonderes Augenmerk sei hier auf die Generierung probabilistischer Vorhersagen gelegt, mittels derer auch die mit Prognosen einhergehende Unsicherheit abgeschätzt werden kann. Dadurch kann ein Unternehmen weitere Planungssicherheit gewinnen, indem es sich gegen ein bestimmtes Unsicherheitsniveau absichert. Aufbauend auf dem oben skizzierten Optimierungsmodell kann dann ein sogenanntes stochastisches Optimierungsmodell formuliert werden, das einen gegenüber einer gewissen Unsicherheit robusten Produktionsplan erzeugt. Damit ist das Unternehmen auch in unsicheren Absatzszenarien mathematisch garantiert dazu in der Lage, auftretende Nachfrage schnell zu erfüllen.

Julius Mehringer

————————————————————————————————————————————————–

Making the right decisions with mathematical optimization – Decision support along the supply chain

The special characteristic of the ADA Lovelace Center is the combination of competencies in AI research with practical applications. The scientists do not only research in one competence pillar like „Sequence-based Learning“, „Data-centric AI“ or „Trustworthy AI“ but develop and use the methods in different practice-oriented issues.Today, I am pleased to present another guest blog post from an expert at the ADA Lovelace Center focusing on his research. Julius Mehringer leads the application „Adaptive Self-Optimizing Logistic Networks“  and develops suitable mathematical optimization models to enable decisions related to a complex system.

Join me diving into the world of „Mathematical Optimization“ and how it helps to make optimal decisions within complex business processes!

Forecasting and mathematical optimization in practical application

In order to achieve defined business goals, employees need to constantly arrive at promising business decisions. In many cases, estimates about the future can help to make proper planning decisions. Questions such as „What will future demand be?“ or „To likely meet this demand, how do we need to plan our production?“ are tackled in the research field of Prescriptive Analytics – the combined use of forecasting and optimization for decision making.

Optimal production planning for mixed products

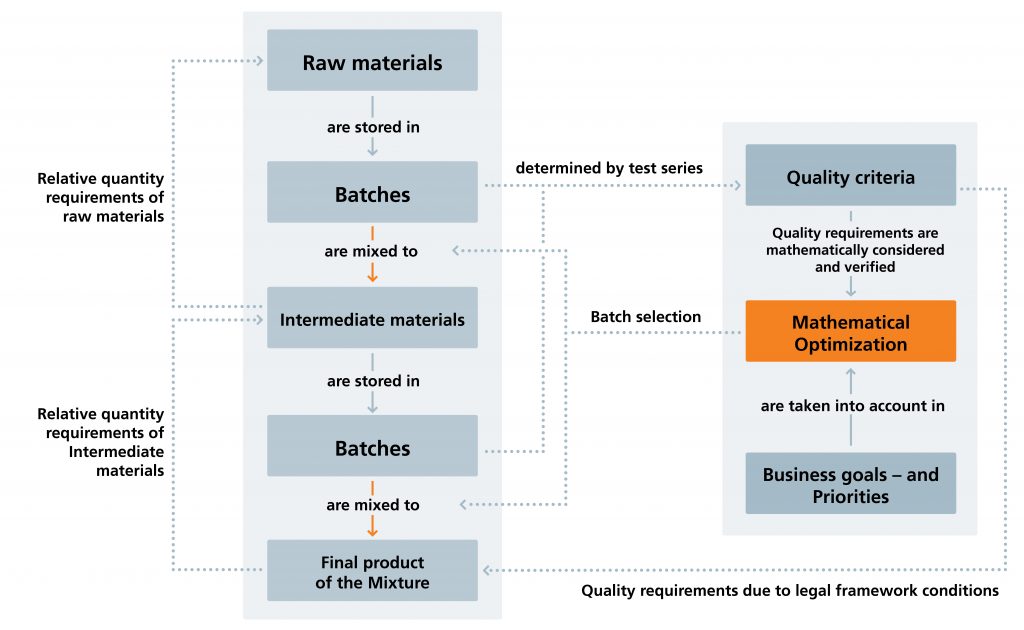
Imagine a model supply chain within a manufacturing company in the processing industry. In this model company, a product is produced by mixing raw materials, which should have a consistent quality. The first step is to solve the mixing problem in such a way that the result is available in an acceptable amount of time. For this purpose, the mathematical structure of the problem was investigated, and it was identified how the time needed solution can be decreased.

Conditions dependent on the production area as well as customer-specific priorities and goals lead to individual characteristics of the mathematical model.

The mathematical model’s individual character  is dependent on the production area-dependent conditions and customer-specific priorities and goals. Different business objectives, such as maximized order coverage, early use of raw or intermediate material batches that would decline in quality if kept for much longer, or customer and order prioritization, can be considered in a prioritized manner in a chain of models that build on one another.

The results of the mathematical optimization provide valuable decision support for the production planner and consequently reduce time and costs for the company. Furthermore, prescient planning enables a more sustainable inventory management.

Forecasting the demand for products

So far, heuristics dominate the estimation of future occurring demand. In order to improve decision making even in scenarios lying in the future, the demand of products can also be forecasted. Depending on the characteristics of the demand patterns, statistical or machine learning methods (e.g. Exponential Smoothing (ETS) or deep autoregressive models (DeepAR)) are able to capture historical demand patterns and extrapolate those patterns to the future. Especially probabilistic forecasts are of relevance, since those can also be used to estimate the uncertainty associated with the obtained forecasts. This allows a company to achieve further planning assurance by protecting itself against a certain level of uncertainty. Then, combining the forecasting model and the optimization model outlined above, a so-called stochastic optimization model can be formulated. It generates a production plan robust against a certain level of uncertainty. In this way, the company is mathematically guaranteed to be able to quickly meet demand as it arises, even in uncertain demand scenarios.

Julius Mehringer